

The work of Perelman (2002, 2003 Robinson 2003) established a more general result known as the Thurston's geometrizationĬonjecture from which the Poincaré conjecture immediately follows. However, Dunwoody's manuscript was quickly found to be fundamentally flawed (Weisstein 2002). In April 2002, M. J. Dunwoody produced a five-page paper that purports to prove the conjecture. The Clay Mathematics Institute included the conjecture on its list of $1 million prize problems. Smale subsequently extended his proof to include all ). Medal), was demonstrated by Zeeman (1961), The proof has not yet been fully verified), was proved byįreedman (1982) (for which he was awarded the 1986 Fields Is trivial, the case is classical (and was known toġ9th century mathematicians), (the originalĬonjecture) appears to have been proved by recent work by G. Perelman (although Proposed another incorrect proof, then discovered a counterexample (the Whitehead Poincaré subsequently found a counterexample. P. 370), stated four years prior to formulation of his conjecture, and to which One of the first incorrect proofs was due to Poincaré himself (1953, In the understanding of the topology of manifolds The Poincaré conjecture has proved a thorny problem ever since it was first proposed, and its study has led not only to many false proofs, but also to a deepening The generalized statement reduces to the original conjecture for. Is homotopy-equivalent to the -sphere iff (Poincaré 1953, pp. 486 and 498), and subsequently generalized to the This conjecture was first proposed in 1904 by H. Poincaré Says that the three-sphere is the only type of bounded three-dimensional space possible

Is simply a generalization of the usual sphere to oneĭimension higher.
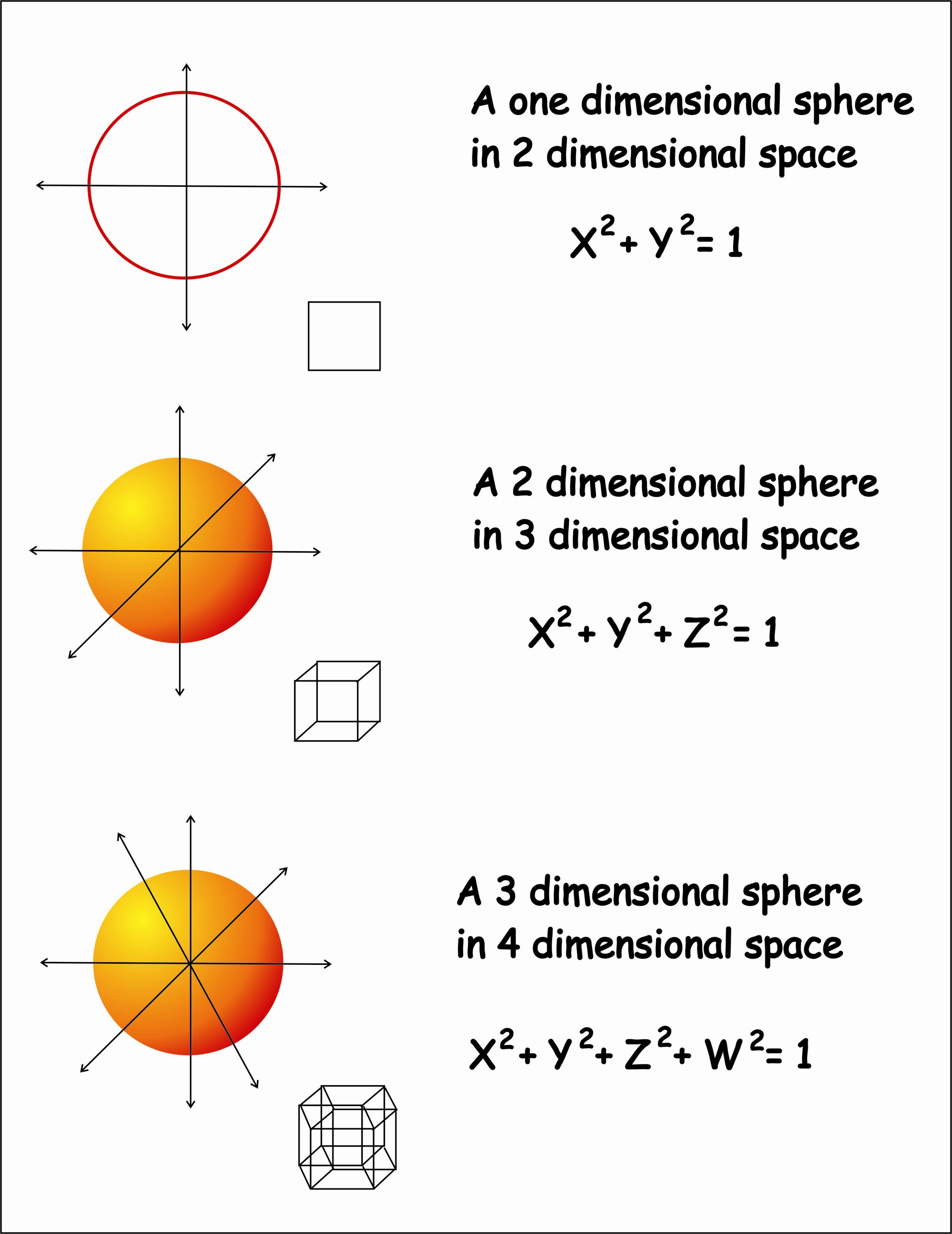
To the three-sphere (in a topologist's sense), where a three-sphere In its original form, the Poincaré conjecture states that every simply connected closed three-manifold is homeomorphic


 0 kommentar(er)
0 kommentar(er)
